Publications
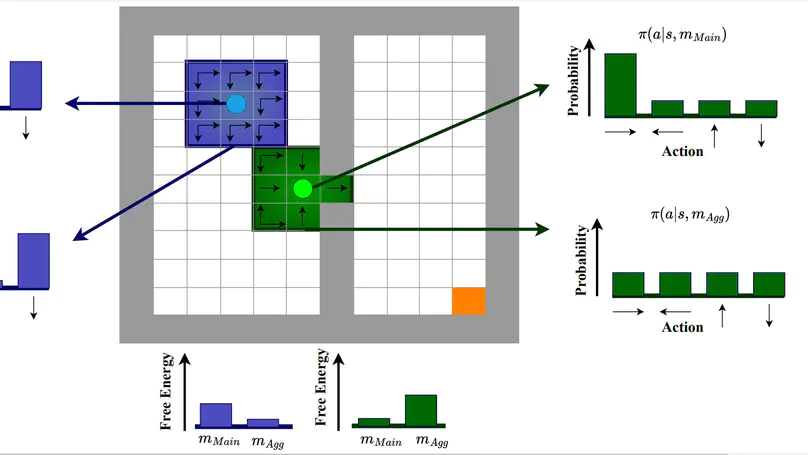
Reinforcement Learning (RL) is mainly inspired by studies on animal and human learning. However, RL methods suffer higher regret in comparison to natural learners in realworld tasks. This is partly due to the lack of social learning in RL agents. We propose a social learning method for improving the performance of RL agents for the multi-armed bandit setting. The social agent observes other agents’ decisions, while their rewards are private. The agent uses a preference-based method, similar to the policy gradient learning method, to find if there are any agents in the heterogeneous society worth learning from their policies to improve their performance. The heterogeneity is the result of diversity in learning algorithms, utility functions, and expertise. We compare our method with state-of-the-art studies and demonstrate that it results in higher performance in most scenarios. We also show that performance improvement increases with the problem complexity and is inversely correlated with the population of unrelated agents.
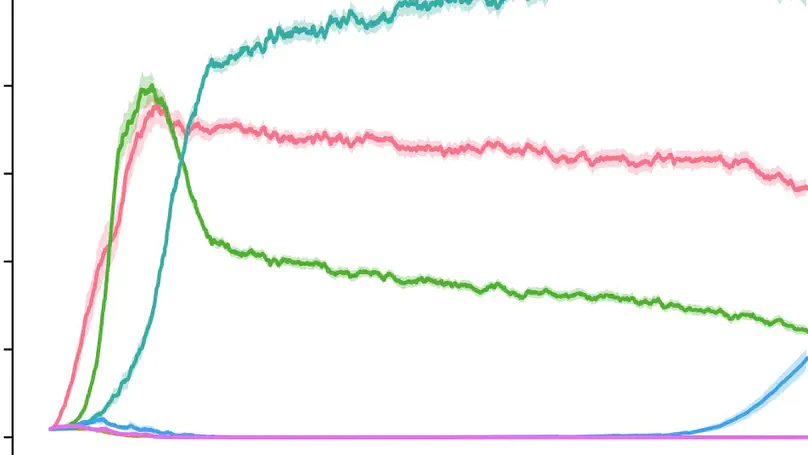
Reinforcement Learning (RL) is mainly inspired by studies on animal and human learning. However, RL methods suffer higher regret in comparison to natural learners in realworld tasks. This is partly due to the lack of social learning in RL agents. We propose a social learning method for improving the performance of RL agents for the multi-armed bandit setting. The social agent observes other agents’ decisions, while their rewards are private. The agent uses a preference-based method, similar to the policy gradient learning method, to find if there are any agents in the heterogeneous society worth learning from their policies to improve their performance. The heterogeneity is the result of diversity in learning algorithms, utility functions, and expertise. We compare our method with state-of-the-art studies and demonstrate that it results in higher performance in most scenarios. We also show that performance improvement increases with the problem complexity and is inversely correlated with the population of unrelated agents.